2025-03-21

The 2025 ICPC Asia Pacific Championship 参加記 (k1suxu視点)

これはなに
ICPCってなに？？
経緯
渡航前
Day 1
Day 2
Day 3
- コンテスト開始
- コンテスト後
Day 4
全体の感想
おわりに

これはなに

先日、シンガポールで行われていたThe 2025 ICPC Asia Pacific Championshipにチーム2getとして出場しました。チームメンバーは、k1suxu(私)、bayashikoさん、krpsさんの3人です。また、コーチとしてsuzukenさんが帯同してくださいました。去年、playoffまで出場しているにもかかわらずICPCについて何もブログに残さなかったことをちょっとばかし後悔しているので、今年こそはと思い、ブログに書き起こすことにしました。

ICPCってなに？？

年一で行われる、競技プログラミングの大学対抗大会です。世界中の大学から選りすぐりの競プロエリートたちが集い、アルゴリズムとデータ構造に対する知見・数学的思考力・プログラム実装能力を競い合います。
cf. 日本語公式サイト
cf. 英語公式サイト
cf. ルール(より詳しくはサイト内のJudging Detailsを読むのがいいかも？)

経緯

今年の国内予選では、チーム全体であり得ない大冷えをかましてしまい、弊大学の他のチームの健闘もあり横浜 regionalへの出場権を掴み損ないました。チームメイトのbayashikoさんがラストイヤーだったことも相まって、「この結果で終わるのは嫌だ」というチームメイト全員の総意から台湾 regionalに海外遠征をし、playoffへの出場権を獲得しました(cf. 台湾 regionalの順位表(我々は18位))。

渡航前

自分含めチームメンバー全員が忙しかったため、チーム練はあまりできませんでした。唯一やったことと言えば今年の横浜大会のバチャをやったくらいで、結果7完、playoffに出れるか否かギリギリ位という感じでした。

Day 1

空港に集合して香港経由でシンガポールに向かいました。使用した航空会社はcathay pacificで、LCC直行便よりも安く機内食ありのフルキャリアで、とても快適でした(LCCで7-8時間座り続けるよりはトランジットありの方が休憩を挟めて楽なのかなという所感)。途中、羽田空港ではIAEPCのオンサイトコンテストに参加される予定の選手の方々に偶然遭遇し、日本有数の実力者を目の前にして勝手に感動するとともに、モチベが向上しました。機内食でハーゲンダッツが出て驚いたりもしました。

夜9時頃にホテルに到着して、コンビニで水等の生活必需品を買い出し、その日はすぐに寝ました。

Day 2

2日目は開会式とプラクティスです。朝ごはんはホテルのビュッフェスタイルで、おいしい料理が多く、朝から上機嫌でした。開会式とプラクティスの間の空き時間にlate registrationを済ませ、スポンサーブース訪問をして、大会Tシャツや企業グッズ(Tシャツ・エコバッグ・水筒・トランプ etc...)をこれでもかというほどたくさん貰いました(スポンサー企業の方々に大いなる感謝...ありがとうございます！！)。

コンテスト会場ではスポンサーブースでもらえる水筒以外で飲料水を持ち込むことが禁止されていました(!?!?)。ちなみに、ペットボトルが支給されるとかもなく、持参したスポンサー水筒に補充する以外では飲料水が手に入らないという形式でした。

我々はスポンサーブースでたまたま水筒を受け取っていたので一安心...と思ったのもつかの間、運営の方から「その水筒は認めない」という旨の注意を受けました(スポンサーブースで受け取ったはずなのになんてこった！)。今こそ英語力を活かすとき！という思いで、その水筒をスポンサーブースで受け取った旨、その水筒が特に名指しで禁止されているようなルールはどこにもない旨等を主張し続けていたら、最終的にはその水筒のコンテスト会場への持ち込みが許可されました(やったね)。

運営側が想定していた水筒はHuawei or JaneStreetの2種類だったそうですが、そのどちらにも該当しない水筒を他のスポンサーが配っていたことを運営側が把握しきれていなかったようです。まあ、あれだけたくさんのスポンサーがいたら把握漏れがあっても致し方ないと思います...運営の皆様いつもありがとうございます..！！

プラクティスの問題はAが謎問、Bがいつものインタラクティブのやつ、C, Dが去年のplayoffの問題だったと思います(順番は間違えているかも)。Dが去年、解法は出ているが実装が間に合わなかった問題で、当時はチームメイトのhotmanさんが解いていたのですが、このプラクティスの時間で自分自身の手で解くことができ(チームメイトのキーボードへの慣れ等を優先していたため実装はしていませんが)、自分の成長を感じられてうれしかったです。

この日の夜ご飯はなんかいい感じのホテルのビュッフェだったのですが、とてもおいしく感動しました。

夜ご飯の設定時間が結構長めで暇を持て余していると、コーチのsuzukenさん達に、「近くにマーライオンがあるから見に行かないか」と誘っていただき、夕食会場を抜け出してマーライオンやマリーナベイサンズを見に行きました。

Day 3

コンテスト本番です。朝ごはんを食べて送迎バスに乗ってコンテスト会場に向かいました。

コンテスト開始

難易度はばらばらなのでチームメイト3人で前・真ん中・後ろから読み進めることにしていました。パソコンのセットアップは慣れている僕がすると決めており、自分はパソコンのセットアップ後真ん中から問題を読み進めました。

問題を読んでいるとLにFAが出たのでとりあえず私が読みます。私たちのチームは、典型考察・天啓をbayashikoさんが、天才adhocをkrpsさんが、ARC辺りの微adhoc考察・数学考察を含む高難易度を私が担当することになっていました。しかし、APAC(この大会の略称)ではどの問題も骨が折れるものばかりであり、最初の問題から多少難しいことが予想されるので、解かれている問題が急激に増えない限り私が問題考察を担当するのがいいだろうと考え、L問題を私が奪う形になりました。隣接している人々の差に着目して処理してあげれば簡単に解けそうなのでその通りに実装します。しょうもないバグで1ペナしてしまいましたが、無事ACしました(0:33(+1))。

次に、A, G, JにFAが出たのでそれら3問を並列に考察していきます。J問題は細かい部分の設定が複雑そうなので、読解をチームメイトに任せ、私はA, G問題の考察を行います。A問題では、数え上げるべき位置関係が高々数種類しかないことに気づいたのでそれぞれを独立に解けばよく、あとは算数で終わりでした(1:03 AC)。

次にG, Jを考えます。Gは前から貪欲に一致させるのがよさそうです。ある程度実装を頑張って提出するとWAが返ってきます(こういう問題でWAは心がつらい...)。いったんJに移り頭をリフレッシュさせることにして、J問題を考察するとここで私がとんでもない嘘解法を出してしまい、無駄なライブラリ写経を発生させてしまいました...(本当にごめん...)。

J問題の実装をある程度完了させたところでその解法があからさまに嘘解法であることに気づき絶望しましたが、J, G問題は自分一人が考察していためチームメイトはその他の問題に分散しており、また実装キューが詰まっているわけでもなかったため不幸中の幸いだと思いながらG問題に再度挑戦します(本当は実装キューが詰まる位の考察力を手にしたい、という気持ちは今は隅に置いておきます)。

G問題でランダムケースを愚直解と照らし合わせ、修正作業を繰り返し、コーナーケースの改善等を行い、遂に通りました(2:25(+2))。2ペナしてしまいましたが、ほかのチームの状況も見てみると、特段ペナルティが多いわけでもなく少し安心していると、Jがとてもシンプルな区間dpであることに気づきます(問題の制約的に区間dpじゃないかと問題を見た瞬間にbayashikoさんと話していたので、区間dp方針を詰めなかったことをとても後悔しました...)。

Jの実装はとても簡単なので実装するとすぐにAC(2:39)。

さて、ここから地獄が始まります。

D, Hが解かれており、Dが私の得意枠(数学)、Hがbayashikoさんの得意枠(天啓インタラクティブ)だったため、D, Hに分かれて考察を始めました。

Dはハノイの塔の途中状態が与えられる(この状態はクエリによって変化する)ので、その状態での最小手数を計算してねという問題でした。どう見てもセグ木に乗る見た目をしています。考察を進めると、マージ計算量が少し重いモノイドではあるが、取り合えずセグ木に乗せられることが分かりました。Dの考察は終了しているのですが、せめて6完しないとWorld Finalは絶望的な状況だったので、分かればより実装が簡単であろうH問題を優先する判断をし、チームメイト全員でH問題に挑戦することにしました。

bayashikoさんが惜しい解法をいくつも考案してくれたのですが、どれも一歩及ばず特定のケースで解けなくなるという状況が続き、私も違う方向性から考察することを繰り返していたのですが同様に一歩足りないという状況が続きました。

そんな地獄時間が続いたのち、コンテストは終了してしまいました。

Dの解法は合っていたようですが、Hの解法はそもそもまったく違う方針が必要だったらしく、自分たちの試行していた時間がとても空虚に感じられました...悲しい...

コンテスト後

順位表凍結解除*1を楽しみ、夕食を食べ、次の日のUSS(Universal Studio Singapore)に備え早めに寝る...わけもなく体力の限界を感じながらもABCに参加しました。

Day 4

この日はExcursionで、USSに行きました。日本にはないトランスフォーマーのアトラクションや、Xで盛り上がりを見せていたジェットコースターなどに乗り、とても楽しかったです。

全体の感想

今年はコンテストを含むすべての進行がとてもスムーズで、ストレスフリーのとても気持ち良いコンテストでした！去年のベトナムのワクワクも今振り返れば楽しかったんですが、こういう安定したコンテストもこれはこれで勿論楽しい。運営の皆様ありがとうございました！！

おわりに

コンテスト自体の成績としては大きな心残りがあるものの、大学1年2年と、2年間連続で海外大会に出場できたことにはとても満足しています。貴重な機会を提供してくださっているICPC 運営及びそのスポンサー様に感謝申し上げます。

来年こそはWFに行けるよう、これからも頑張ります。

ふと思って即席で書き上げたブログですので、誤植が多数あるかと思われます。何か誤植等発見した方は是非XのDM等で教えていただけると幸いです。

ここまで読んでいただきありがとうございました。

*1:ICPC ではコンテスト残り 1 時間時点で順位表の更新が止まり、それ以降の他チームの提出の正否は分からなくなります(順位表凍結)。凍結を解除していく瞬間は、そのコンテストの最終的な順位が決定される瞬間でもあり、ICPCで最も盛り上がる瞬間だと感じています(実際とても楽しい)。

2022-11-02

APIO2022に参加しました！！

　幸いにも今年は募集枠が多かったため、今年のAPIO(Asia Pacific Informatics Olympiad)2022Egyptに出場することができました。競技の感想について残します。コードにおけるマクロに関しては

k1suxu.hatenablog.com

の「テンプレートの作製」の欄をご参照ください。
書くだけ書いて投稿してなかったことに気付いたので2年越しに公開しました。

当日の流れ

競技前

　当日はゆっくり9時ごろに起きて競技開始時間の13:00に向けてご飯を食べたりしました。

競技開始

　APIOでは、問題、サンプル、各種コードなどがzipファイルなどにまとまった状態で掲示されるので、とりあえずそれらをダウンロードしてフォルダに入れました。
　とりあえず問題を一通り読みます。marsの問題文の意味が分からなくて焦りながら、とりあえずgame, permの読解に移ります。とりあえず問題設定は把握したのですぐに考察に移りました。以下は自分が解いた問題の順番とその解法です。

perm 91.36点

　これは部分列のうち単調増加であるような数が $K$ 個となるような順列 $A$ を構成してほしいということです。こういった構築系は二進数にするのがいいという典型があるのでとりあえず二進数で考えてみると、ある時点でどの要素よりも大きいような要素を右に入れると条件を満たすような部分列の個数は2倍になって(手順1)(1bit右にずらす)、右に入れてから左に入れると元の通り数を $X$ とすると、 $2X+1$ となる(手順2)(1bitずらしてから+1)ことがわかりました。ということでビットが立っている位置を見つけたら手順2を、そうでなければ手順1を行うようにするとうまく構成できます。実際には再帰的に求めることで構成しました。
提出コードは以下です。

vector<int> construct_permutation(ll k) {
    k--;

    if(k == 0) return {};
    
    if(k == 1) return {0};

    vector<int> ret;

    if(k%2 == 1) {
        vector<int> ret = construct_permutation(k/2+1);
        ret.push_back(ret.size());
        return ret;
    }else {
        vector<int> ret = construct_permutation(k);
        ret.insert(ret.begin(), ret.size());
        return ret;
    }

    assert(false);
    return {};
}

game 30点

　部分点の1~3については毎回DFSをすればいいことはすぐにわかったので実装しました。まず、initが呼び出されるタイミングで、初期状態のテレポーターを示す辺を張り、add_teleporterが呼ばれるたびに辺を追加しDFSによって判定しました。判定においては、 $0\leqq{i}\leqq{j}\lt k$ なる頂点組 $(i, j)$ であって、 $j$ から一つ以上の辺を通って $i$ に行けるようなものが存在するかどうかを判定できればいいです。より具体的には頂点0からDFSをし、現在の経路内にある頂点をsetで管理し、頂点番号が $k$ よりも小さいような頂点に来たらset.findで既出判定を行うことで判定できます。
提出コードは以下です。

vvi g;
vector<bool> can;
int nn, kk;

void init(int n, int k) {
    g.resize(n);
    nn = n;
    kk = k;
    FOR(k-1) g[i].push_back(i+1);
    can.resize(n, false);
}

vector<bool> done;
set<int> st;

int dfs(int v) {
    if(can[v]) return true;

    done[v] = true;
    st.insert(v);
    for(auto e : g[v]) {
        if(e < kk && st.find(e) != st.end()) return can[v] = true;
        else if(!done[e]) {
            if(dfs(e) == 1) return can[v] = true;
        }
    }

    st.erase(v);
    return can[v];
}

int add_teleporter(int u, int v) {
    done.assign(nn, false);
    st.clear();
    g[u].push_back(v);
    return dfs(0);
}

mars 14点

　ここにきて問題文の意味が理解できなかったmarsの読解に入ります。簡潔に言えば、「連結成分の個数を数えたいけどメモリの制限が厳しいからデータをうまく圧縮してね」という問題です。普段こういった形の問題を解く機会はなかったので、読解に苦戦してしまいましたが、非常に勉強になりました。
　簡単にわかることとして、盤面の情報をbitで表したものを左上に左上に渡していけばいいのでその方針で実装すると14点が取れました。連結成分の個数は簡潔にBFSで数え上げました。
提出コードは以下です。

ll cal(string s, int n) {
    vector<vector<bool>> grid(n, vector<bool>(n, false));
    rep(i, n) {
        rep(j, n) {
            if(s[i*n+j] == '1') grid[i][j] = true;
        }
    }

    vector<vector<int>> dist(n, vector<int>(n, -1));

    auto bfs = [&](int X, int Y) -> void {
        dist[X][Y] = 0;
        queue<pii> que;
        que.emplace(X, Y);
        while(que.size()) {
            int x, y;
            tie(x, y) = que.front();
            que.pop();

            rep(d, 4) {
                int nx = x + dx[d];
                int ny = y + dy[d];

                if(nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
                if(dist[nx][ny] < 0 && grid[nx][ny]) {
                    dist[nx][ny] = dist[nx][ny] + 1;
                    que.emplace(nx, ny);
                }
            }
        }
    };

    ll ans = 0;

    rep(i, n) {
        rep(j, n) {
            if(grid[i][j] && dist[i][j] < 0) {
                bfs(i, j);
                ans++;
            }
        }
    }

    return ans;
}

string to_bit(ll n) {
    string ret(100, '0');
    rep(i, 60) {
        if(n >> i & 1) ret[i] = '1';
    }
    return ret;
}

string process(vector<vector<string>> a, int i, int j, int k, int n) {
    int dim = 2*k+1;
    string ret(100, '0');
    rep(id, dim) {
        rep(jd, dim) {
            rep(ii, 3) {
                rep(jj, 3) {
                    ret[(id + ii) * (dim + 2) + (jd + jj)] = a[ii][jj][id * dim + jd];
                }
            }
        }
    }

    // cout << ret << endl;

    if(k == n - 1) {
        return to_bit(cal(ret, dim+2));
    }else {
        return ret;
    }

    assert(false);
    return "";
}

　marsに関してはこれ以上の部分点を取ることはできませんでした。

game 60点

　30点を取ったときの考察にある「 $i\leqq{j}\lt k$ なる頂点組 $(i, j)$ であって、 $j$ から一つ以上の辺を通って $i$ に行けるようなもの」という部分を高速化したいなと思いました。ここで、説明の都合上、順辺を張ったグラフを $G$ , 逆辺を張ったグラフを $G'$ とします。ある頂点 $v$ について $G$ 上で到達可能な頂点のうち、 ${0\leqq{i}} \lt k$ を満たすものの最小値を $min_v$ とし、 $G'$ 上で到達可能な頂点のうち、 ${0\leqq{i}} \lt k$ を満たすものの最大値を $max_v$ とします。
するとこの問題は、 $min_v\leqq{max_v}$ を満たすような頂点 $v$ が存在するかというものに帰着します。
　あとはうまいこと必要部分のみを更新するように実装するだけです、少し複雑ですが以下の実装を参考にしてください。
　正直この提出で60点をとれるとは思っていなかったのですが、 $k\leqq{1000}$ がうまく効いてくれたおかげで得点を伸ばすことができました。

vvi g, rg;
vector<int> from, to;
int nn, kk;

void init(int n, int k) {
    g.resize(n);
    rg.resize(n);
    nn = n;
    kk = k;
    FOR(k-1) g[i].push_back(i+1);
    FOR(k-1) rg[i+1].push_back(i);
    
    to.assign(n, INF);
    from.assign(n, -1);
    FOR(k) from[i] = i;
    FOR(k-1) to[i] = i+1;
}


void dfs1(int v, int now, int& mnto) {
    from[v] = now;
    chmin(mnto, to[v]);

    for(auto e : g[v]) {
        if(from[e] < now) {
            dfs1(e, now, mnto);
        }
    }
}

void dfs2(int v, int now, int& mxfrom) {
    to[v] = now;
    chmax(mxfrom, from[v]);

    for(auto e : rg[v]) {
        if(to[e] > now) {
            dfs2(e, now, mxfrom);
        }
    }
}

int add_teleporter(int u, int v) {
    if(u < v && v < kk) return 0;

    if(u == v) {
        if(u < kk) {
            return 1;
        }else {
            return 0;
        }
    }

    g[u].push_back(v);
    rg[v].push_back(u);

    int mxfrom = -1, mnto = INF;

    if(v < kk) {
        if(to[u] > min(to[v], v)) {
            dfs2(u, min(to[v], v), mxfrom);
        }
    }else {
        if(to[u] > to[v]) {
            dfs2(u, to[v], mxfrom);
        }
    }
    if(u < kk) {
        if(from[v] < max(from[u], u)) {
            dfs1(v, max(u, from[u]), mnto);
        }
    }else {
        if(from[v] < from[u]) {
            dfs1(v, from[u], mnto);
        }
    }

    if(to[u] <= mxfrom || mnto <= from[u] || to[v] <= mxfrom || mnto <= from[v]) {
        return 1;
    }

    return 0;
}

競技終了

　ここまで合計得点 $14+60+91.36=165.36$ で競技が終了しました。最終順位は国内16位(同順位5人)銅メダル相当という結果になりました。
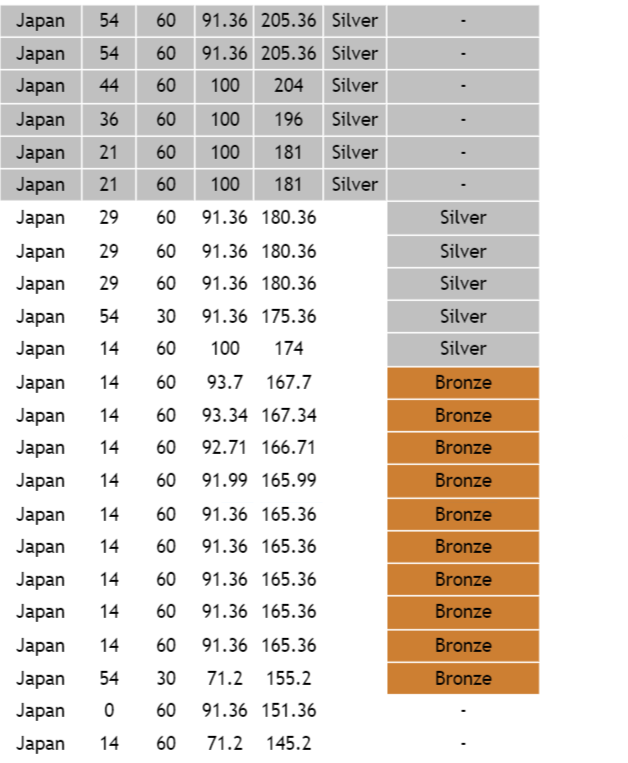
ちなみに、permは既出だったらしいです(悔しい) atcoder.jp
　私にとってはこれが最後の情報オリンピック関連大会だったので、いい結果が残せてよかったです。大学ではICPCにも出たいですね。

2022-05-15

青色コーダー(AtCoder)になりました！！

　初めまして、趣味で競技プログラミングをやっているk1suxuと申します。言語は主にC++を使用しています。先日のAtCoder Beginner Contest 251にて、幸いにも初黄パフォを出すことができ、念願の入青を果たしました。自分の進捗を残すためにもブログに書き起こしてみます。

競技プログラミングを始めて約一年、初の黄パフォとともに念願の入青です！！
k1suxuさんの成績:140位
パフォーマンス:2335相当
レーティング:1505→1621 (+116) :)
Highestを更新し、2 級になりました！#AtCoder #ABC251 #パナソニックグループプログラミングコンテスト2022 https://t.co/g6q5FkQCFa pic.twitter.com/wpCq1NGIPZ
— k1suxu (@k1suxu) 2022年5月14日

現在のAtCoderの進捗状況

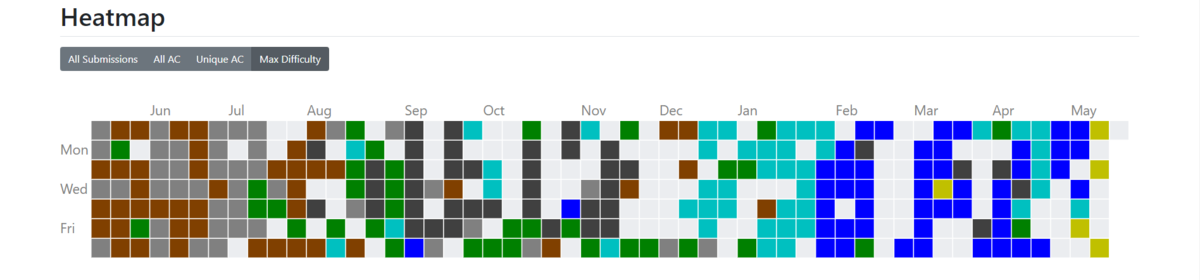最近は一気に青色を解き進めた後に少しずつ黄色を解いています。

青色になるまでに学んだこと

　この章では、私が青色になるまでに学んだ知識について列挙しています。一部抜けがあるかもしれませんがご了承ください。また、色ごとの勉強方法やその色の時期に何を学んだかなどについては、次の章をご参照ください。

1.数学的な知識

青色になるまでに学んだ数学的な知識は以下の通りです。

高校数学

　競技プログラミングを始めたのが高校2年生の4月であって、今も高校生なので、特に追加で学んだことはないのですが、競技プログラミングで重要だと思う分野は以下です。

・ベクトル(平面、空間)

・初等幾何(三角関数、三平方の定理、多角形の面積など)

・初等関数(n次関数や三角関数、指数対数関数などといった関数の概形に関する知識)

・方程式(問題文に対して適切に未知数を定め、計算式にまとめる能力がしばしば求められます)

・不定方程式(不定方程式の考え方を用いて、二つの未知数に対して一つを全探索してもう一つを求めるというような考察が必要となることがあります)

・数え上げ(場合の数)(いわゆる写像12相などです)

・確率(条件付確率や包除原理など)

・期待値(特に期待値の線形性)　私の苦手分野です。

・数列(等差数列、等比数列、漸化式、特性方程式、一般項や総和、級数の公式など)

・複素数平面(図形問題を複素数平面上で解くとうまくいったりします)

その他

・行列の基礎的な知識(行列を用いて連立方程式の解を求める方法、行列式、転置、逆行列)

・群論における基礎、特に演算子の定義やモノイドなど

・オーダー表記(計算機科学？)による計算量、メモリ量の見積もり

・グラフ理論の基礎

・パスカルの三角形

・フェルマーの小定理(逆元の計算に必要です)

・拡張ユークリッドの互除法(不定方程式の解を一つ求めます)

2.アルゴリズム・データ構造

青色になるまでに学んだアルゴリズム・データ構造は以下の通りです。

DP

・配るDP, 貰うDP, 区間DP, bitDP, 期待値DP, 桁DP, 文字列DPなど

・LCS(Longest Common Subsequences)

・LIS(Longest Increasing Subsequences)

数学

・MOD上での各種計算、高速累乗(繰り返し二乗法)

・逆元の計算

・パスカルの三角形を用いたnCrの計算

・エラトステネスの篩

・Euler Phi

・転倒数

・スライド最小値・最大値

探索法

・順列全探索

・bit全探索

・二分探索

・三分探索

・半分全列挙

グラフ理論

〇最短経路探索

・BFS, DFS

・Dijkstra

・Warshall Floyd

・Bellman_Ford

〇BFS, DFSの応用知識

・Euler Tour

・01BFS

・BFS Tree, DFS Tree

・強連結成分分解 Strongly Connected Components(SCC)

・二部グラフ判定

・LowLink グラフ上の橋、関節点の検出

・木の直径

〇フロー

・最大流(最小カット)問題(Ford_Fulkerson法、Dinic法)　まだコンテストで使ったことはないです。

〇素集合データ構造

・Union Find

・Weighted Union Find 重み付きUnion Findのことです

〇木構造に関するクエリ

・LCA (Lowest Common Ancestor)

・Topological Sort (DAGの判定にも使えます)

・無向最小全域木(Kruskal法、Prim法)

〇区間に対するクエリを高速に答えるデータ構造など

・BIT(Binary Indexed Tree)

・Fenwick Tree

・セグメント木、遅延セグメント木

・Mo's Algorithm

文字列

・Z_Algorithm

・Rolling_Hash

・ランレングス圧縮

　これらのアルゴリズムは引数を何らかの配列にすることで文字列以外にも適用できます。例えばランレングス圧縮の場合、c++では以下のように実装できます。

▶クリックで展開

template<typename T>
vector<pair<T, int>> run_length_encoding(vector<T> s) {
    T need = s[0];
    int cnt = 0;
    vector<pair<T, int>> ret;
    for(T c : s) {
        if(c == need) {
            cnt++;
        }else {
            ret.emplace_back(need, cnt);
            need = c;
            cnt = 1;
        }
    }
    if(cnt != 0) ret.emplace_back(need, cnt);
    return ret;
}

その他

・累積和

・imos法

・座標圧縮

・マンハッタン距離の性質(45度回転)

・しゃくとり法

・調和級数を用いた計算量解析

2.ライブラリの整備

テンプレートの作製

　コンテストに出るにあたりテンプレートファイルを作成しました。現在使用しているものは以下です。特にfor文をマクロで短縮するのはおすすめです。

▶クリックで展開

#include <bits/stdc++.h>
using namespace std;

#define rep(i,n) for(int i = 0; i < (int)n; i++)
#define FOR(n) for(int i = 0; i < (int)n; i++)
#define repi(i,a,b) for(int i = (int)a; i < (int)b; i++)
#define pb push_back
#define m0(x) memset(x,0,sizeof(x))
#define fill(x,y) memset(x,y,sizeof(x))
#define bg begin()
#define ed end()
#define all(x) x.bg,x.ed
//#define mp make_pair
#define vi vector<int>
#define vvi vector<vi>
#define vll vector<ll>
#define vvll vector<vll>
#define vs vector<string>
#define vvs vector<vs>
#define vc vector<char>
#define vvc vector<vc>
#define pii pair<int,int>
#define pllll pair<ll,ll>
#define vpii vector<pair<int,int>>
#define vpllll vector<pair<ll,ll>>
#define vpis vector<pair<int,string>>
#define vplls vector<pair<ll, string>>
#define vpsi vector<pair<string, int>>
#define vpsll vector<pair<string, ll>>

template<typename T>
void chmax(T &a, const T &b) {a = (a > b? a : b);}
template<typename T>
void chmin(T &a, const T &b) {a = (a < b? a : b);}

using ll = long long;
using ld = long double;
using ull = unsigned long long;

const ll INF = numeric_limits<long long>::max() / 2;
const ld pi = 3.1415926535897932384626433832795028;
const ll mod = 1e9 + 7;
int dx[] = {-1, 0, 1, 0, -1, -1, 1, 1};
int dy[] = {0, -1, 0, 1, -1, 1, -1, 1};

void solve() {

}

signed main() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    solve();
    return 0;
}

現在使用しているライブラリ

　前述したアルゴリズムたちにあるものはほぼすべてライブラリ化しています。その他持っているライブラリは以下です。

・構造体：有理数(分数)
・構造体：行列
・素因数分解
・商(整数除算)の列挙
・幾何ライブラリ
->多角形の面積や内外判定など多数

色ごとの勉強

　この章では、私が青色になるまでの色の遷移とその時々にしていた勉強について記述しています。具体的に何を学んだかについては前章をご参照ください。

灰～茶(2021年4月24日～2021年6月13日)

　私がプログラミングそのものの勉強を始めたのは2021年の3月辺りで、その約1か月後に友人に教えてもらったことをきっかけにAtCoderに登録し、競技プログラミングを始めました。当時私はPythonで競技プログラミングしており、多重配列の入力の受け取りや初期化に苦労してた記憶があります。初参加のABC199では2完にとどまりました(当時の私は計算量という概念を知らず、C問題で一生TLEしていました...)。この頃は特に競技プログラミング向けの勉強はしておらず、ひたすらプログラミングの基礎に触れるという感じでした。計算量について少しだけ学びましたが、「ソートって時間かかるんだ。へ～。」程度にしか思っていませんでした。もともとタイピングはそれなりに速かったので、簡単な問題を早く解くことのみに専念していました。

茶～緑(2021年6月13日～2021年9月11日)

　茶色になってからも数か月は、灰色を虚無埋めしていました。7月ごろになり、学校が夏休みに入ったころ、E869120さんの「レッドコーダーが教える、競プロ・AtCoder上達のガイドライン」という記事を見たことをきっかけにアルゴリズムの面白さに引き込まれました(本当におすすめでとても為になる記事です。ぜひ検索してみてください)。そこからはBFSやDFSなどの基礎的なアルゴリズムを学びつつ、AOJ(AiZU ONLINE JUDGE)などを利用してライブラリの整備などをしていました。そうしている間に緑色になりました。

　ここまでで最短経路アルゴリズム、nCr, nPr, nHrなどのライブラリが整いました。

緑~水(2021年9月11日～2022年1月30日)

　ちょうど緑色になったころ、日本情報オリンピック(JOI)の存在を知り応募しました。一次予選突破が確定したあたりからはJOIの過去問をといていました。私にとっては最初で最後のJOIだったので、この頃はJOI二次予選突破を第一目標に精進していました。今年は例年よりも定員が多かったため、無事に二次予選を突破し、本選に進むことができました。

　JOIが一段落ついたので高校二年生の冬休みはAtCoderに傾倒することにしました。むやみやたらに簡単な問題を解いても成長しないだろうということは経験でわかっていたので、自分の得意不得意やコンテストでの動きについて分析してみることにしました。分析してみた結果当時の私はDPに弱く、早解きはできるが、difficulty*1が緑色以上の問題に対してACできていないということがわかりました。また、グラフの問題に強いという傾向も見て取れました。

　分析の結果を踏まえてDPを扱う問題を解こうと思いEDPCを少し解き進めました。これにより、DPの基礎を学ぶことができました。また、緑色以上の問題を安定して解けるようになることを目標にABC中の緑色の問題を埋めてみることにしました。緑色が安定してきたら、次に水色へと移りました。この頃から、ScrapBoxにて解いた問題の感想や考察の手順、振り返りを始めました。これを始めてから実力が一気に伸びた気がします(知識と解法の点と点が線で結ばれるような感覚です)。水色を60問ほど埋めたあたりでついに水色になれました！！

　この時点で、現在そろっているライブラリの7割ほどは完成しています。具体的には(フローライブラリ, fenwick_tree, rolling_hash, 幾何ライブラリの一部, mo's algorithm, 行列ライブラリ + α以外です)。